-Метки
-Музыка
- Комната-Запутался в себе
- Слушали: 44 Комментарии: 1
- И ЛЕНИН ТАКОЙ МОЛОДОЙ! Иосиф Кобзон
- Слушали: 108 Комментарии: 5
-Интересы
-Друзья
Друзья оффлайнКого давно нет? Кого добавить?
-Kozi-
Agatha_Lastochka
belochka
chrysalide
D_NeeZZ
Diod
Driver2
FORNIT
Glaive_Glaive
greh
i-man3
is-art
Kiruher
KiryAlf
sa1961
Sanefaira
unknown-blind
Артём_Валентинович
Бездушный_убийца
Группа_Аблом
Диод
Затемненная
Зовущая_Шторм
МарленДитрих
Мне_Нужна_Свобода
Московское_метро
Скучающая_Карнимириэ
Головоломки |
Меня на днях попросили решить головоломку.
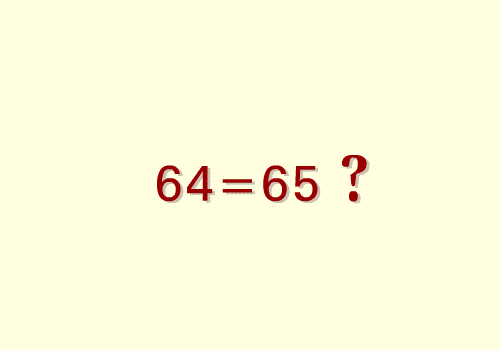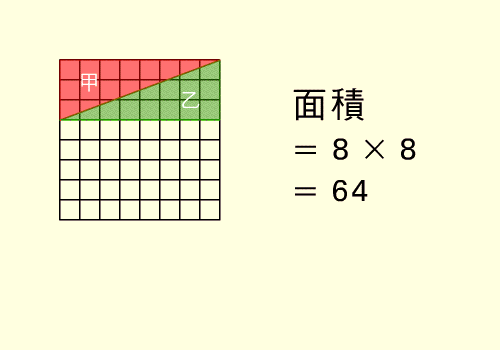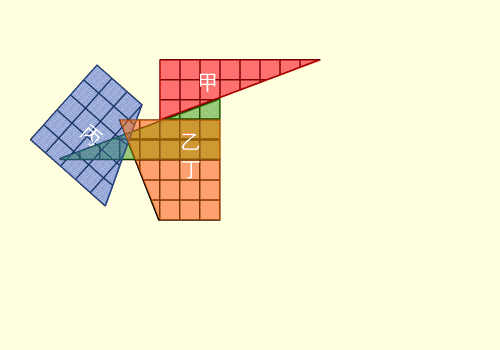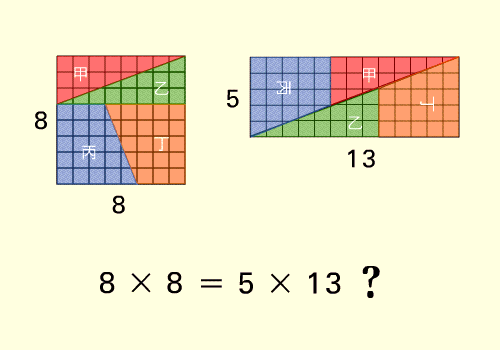
Так вот решая, я наткнулся на ещё одну, похожую.
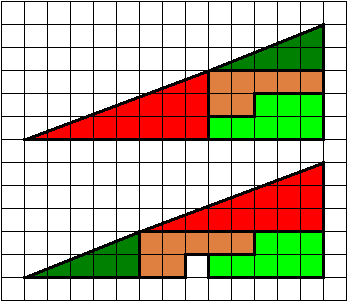
В обеих спрашивается: Откуда берётся ещё один квадрат???
В первой площадь одной фигуры больше чем изначальной, а во второй откуда дырка!
Ответы смотрите в продолжении. ;)
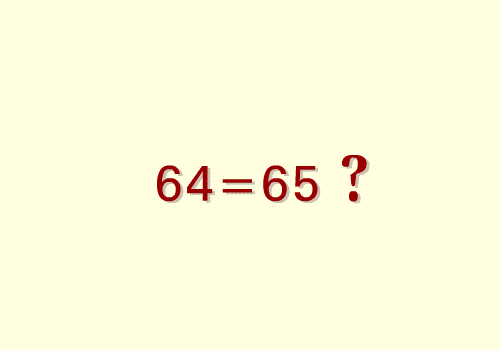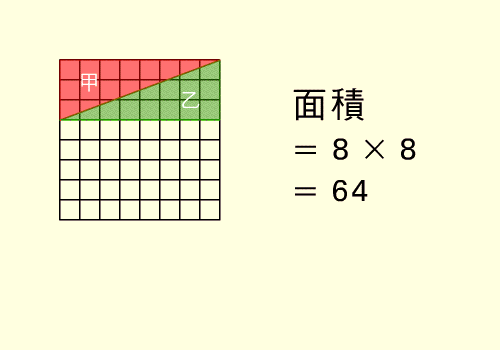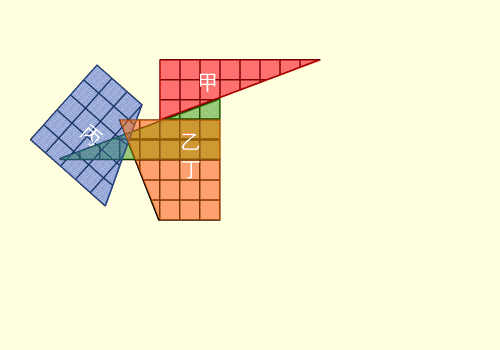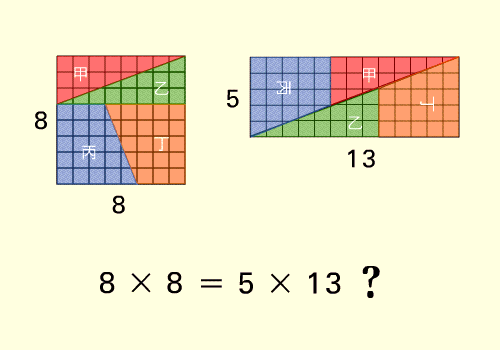
Так вот решая, я наткнулся на ещё одну, похожую.

В обеих спрашивается: Откуда берётся ещё один квадрат???
В первой площадь одной фигуры больше чем изначальной, а во второй откуда дырка!
Ответы смотрите в продолжении. ;)
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |
Нус, начнём с первой!
Я немного перерисовал прямоугольник и пометил жёлтым то место, где "прячется" лишняя клетка!
Да, там разница в углах не большая, но этого хватает, чтобы её не было видно и там помещался квадрат!
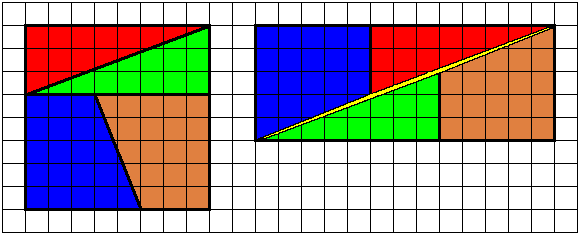
Я немного перерисовал прямоугольник и пометил жёлтым то место, где "прячется" лишняя клетка!
Да, там разница в углах не большая, но этого хватает, чтобы её не было видно и там помещался квадрат!

Посчитаем площади всех фигур!
Несложно видеть, что площади не треугольников равны 7 и 8 квадратов. Теперь посчитаем треугольники. бльшой 8*3/2=12 и маленький 5*2/2=5. Просуммировав получаем 32 квадрата.
А площадь верхнего 13*5/2=32,5 квадрата, а нижнего 31,5 квадрат!
Т.е. площади треугольников - это +-0,5 квадрата от площадей фигур в них входящих. Как такое может быть?
Ответ прост! Дело всё в том, что наклон гипотинузы у большого и маленького треугольника разные и получается, что в первом случае гипотинуза вогнута, а во втором выпукла и поэтому появляется квадрат внизу.
Кто не понял могу разъяснить!
Несложно видеть, что площади не треугольников равны 7 и 8 квадратов. Теперь посчитаем треугольники. бльшой 8*3/2=12 и маленький 5*2/2=5. Просуммировав получаем 32 квадрата.
А площадь верхнего 13*5/2=32,5 квадрата, а нижнего 31,5 квадрат!
Т.е. площади треугольников - это +-0,5 квадрата от площадей фигур в них входящих. Как такое может быть?
Ответ прост! Дело всё в том, что наклон гипотинузы у большого и маленького треугольника разные и получается, что в первом случае гипотинуза вогнута, а во втором выпукла и поэтому появляется квадрат внизу.
Кто не понял могу разъяснить!
Там зазор очень маленький!
Я могу чётко математически сказать каков угол зазора и станет понятно, что его увидеть можно только, если плотно и без зазоров расположить кусочки, что достаточно сложно сделать с бумагой!






